Il trapezio rettangolo è una figura geometrica appartenente alla famiglia dei trapezi, caratterizzata dalla presenza di un angolo retto, che lo rende una figura particolarmente interessante in molte applicazioni geometriche e pratiche. Comprendere le caratteristiche del trapezio rettangolo rispetto a quelle di un trapezio generico è fondamentale per risolvere correttamente problemi di geometria che richiedono calcoli precisi su aree, lati e diagonali. Questo tipo di trapezio si distingue per la semplicità con cui si possono applicare concetti come il Teorema di Pitagora per determinare la lunghezza di ciascuno dei lati e altre proprietà geometriche.
A differenza del trapezio isoscele o del trapezio scaleno, il trapezio rettangolo ha una struttura che rende i calcoli particolarmente semplici. Per esempio, il lato obliquo, insieme alla base minore, forma un triangolo rettangolo con l’altezza, consentendo di applicare facilmente il Teorema di Pitagora per trovare la lunghezza del lato mancante. Ma come si calcola esattamente l’area del trapezio rettangolo? E come è possibile determinare la lunghezza di ciascuno dei lati utilizzando le informazioni fornite dalle basi e dall’altezza? In questo articolo, risponderemo a tutte queste domande e forniremo una guida completa e dettagliata che ti permetterà di comprendere a fondo le peculiarità del trapezio rettangolo.
Esploreremo le differenze tra il trapezio rettangolo e quello generico, vedremo come calcolare l’area e come determinare i lati del trapezio rettangolo grazie al Teorema di Pitagora. Questo articolo è pensato per soddisfare l’esigenza di chi cerca un appunto completo di geometria sul trapezio rettangolo, con spiegazioni dettagliate e semplici da seguire.
Differenze tra trapezio rettangolo e trapezio generico
Il trapezio generico è una figura piana con quattro lati, di cui due paralleli, chiamati basi, e due non paralleli, chiamati lati obliqui. Una delle caratteristiche fondamentali del trapezio è la differenza di lunghezza tra le basi, con la base maggiore tipicamente più lunga della base minore. Tuttavia, nel trapezio rettangolo, una delle principali differenze rispetto al trapezio generico è la presenza di un angolo retto tra una delle basi e l’altezza, che semplifica notevolmente i calcoli geometrici.
Nel trapezio rettangolo, uno dei lati non paralleli coincide con l’altezza, mentre l’altro lato non parallelo forma un triangolo rettangolo con l’altezza e la base minore. Questo significa che è possibile applicare direttamente il Teorema di Pitagora per calcolare il lato obliquo. Di seguito, vediamo alcune differenze chiave tra un trapezio rettangolo e un trapezio generico:
- Angolo retto: il trapezio rettangolo ha un angolo di 90 gradi, mentre un trapezio generico non ha necessariamente angoli retti.
- Lato coincidente con l’altezza: nel trapezio rettangolo, uno dei lati obliqui coincide con l’altezza.
- Teorema di Pitagora: nel trapezio rettangolo è possibile usare il Teorema di Pitagora per trovare la lunghezza del lato obliquo, cosa che non è sempre possibile in un trapezio generico.
Queste caratteristiche rendono il trapezio rettangolo una figura più semplice da gestire dal punto di vista geometrico rispetto al trapezio generico. Ora che abbiamo chiaro cosa distingue il trapezio rettangolo dal trapezio generico, vediamo come si calcola l’area di questa figura.
Come calcolare l’area del trapezio rettangolo
Il calcolo dell’area di un trapezio rettangolo segue la stessa formula generale utilizzata per il trapezio generico. La formula è:
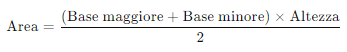
Tuttavia, nel caso del trapezio rettangolo, il fatto che uno dei lati obliqui coincida con l’altezza semplifica i calcoli. Ad esempio, supponiamo di avere un trapezio rettangolo con:
- Base maggiore = 8 cm
- Base minore = 4 cm
- Altezza = 5 cm
Inserendo questi valori nella formula, otteniamo:
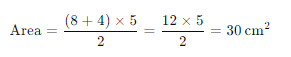
In questo esempio, l’area del trapezio rettangolo è di 30 cm².
Determinare i lati del trapezio rettangolo con il Teorema di Pitagora
Uno degli strumenti più utili per calcolare i lati del trapezio rettangolo è il Teorema di Pitagora. Questo teorema afferma che, in un triangolo rettangolo, la somma dei quadrati dei cateti è uguale al quadrato dell’ipotenusa. Nel contesto del trapezio rettangolo, il lato obliquo e l’altezza formano un triangolo rettangolo con la base minore. Questo significa che possiamo utilizzare il teorema per trovare la lunghezza del lato obliquo.
Supponiamo di avere un trapezio rettangolo con:
- Altezza = 6 cm
- Base minore = 4 cm
Per trovare la lunghezza del lato obliquo, dobbiamo risolvere l’equazione derivata dal Teorema di Pitagora:
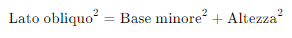
Sostituendo i valori:
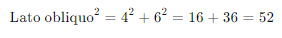
Quindi, la lunghezza del lato obliquo è:
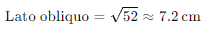
In questo modo, possiamo determinare la lunghezza del lato obliquo utilizzando il Teorema di Pitagora. Questo procedimento può essere ripetuto per qualsiasi trapezio rettangolo, a condizione di conoscere almeno la base minore e l’altezza.
Applicazioni pratiche del trapezio rettangolo
Il trapezio rettangolo trova applicazione in diversi ambiti, dalla progettazione architettonica alla risoluzione di problemi ingegneristici. La sua forma semplice e la facilità con cui è possibile calcolare i suoi lati e la sua area lo rendono una figura geometrica particolarmente utile in contesti pratici. Alcuni esempi di applicazioni includono:
- Costruzione di rampe: la forma di un trapezio rettangolo è spesso utilizzata per progettare rampe, dove l’altezza rappresenta la pendenza e le basi corrispondono al livello superiore e inferiore della rampa.
- Tetti inclinati: molti tetti di edifici sono progettati a forma di trapezio rettangolo, con l’altezza rappresentante la distanza tra il punto più alto e la gronda.
- Sviluppo di progetti di ingegneria strutturale: la capacità di determinare facilmente l’area e i lati del trapezio rettangolo rende questa figura utile per calcolare carichi e pressioni in strutture geometriche complesse.
Conclusioni
Il trapezio rettangolo è una figura geometrica con caratteristiche uniche che lo distinguono dal trapezio generico. Grazie alla presenza di un angolo retto, è possibile applicare il Teorema di Pitagora per determinare con precisione la lunghezza del lato obliquo. Il calcolo dell’area del trapezio rettangolo segue la stessa formula utilizzata per il trapezio generico, ma con la semplificazione offerta dalla coincidenza tra altezza e lato obliquo.
Le applicazioni pratiche di questa figura sono numerose, rendendola una delle più utilizzate in contesti ingegneristici e architettonici. Spero che questo appunto completo di geometria sul trapezio rettangolo ti sia stato utile per comprendere meglio le sue caratteristiche e le sue potenzialità geometriche.
