Il triangolo rettangolo rappresenta una delle forme geometriche più affascinanti e studiate all’interno del vasto panorama della matematica. Con i suoi angoli caratteristici e le proprietà uniche, il triangolo rettangolo trova applicazione in numerosi campi, dalla fisica all’ingegneria, dimostrandosi uno strumento imprescindibile per risolvere problemi pratici e teorici.
In questo articolo, esploreremo a fondo il concetto di area del triangolo rettangolo, offrendo una guida dettagliata che non solo soddisferà la curiosità degli appassionati di matematica ma sarà anche una risorsa preziosa per studenti e professionisti. Attraverso un approfondimento delle formule, esempi pratici e un esercizio illustrato, miriamo a fornire una comprensione completa di come calcolare l’area di questa figura fondamentale.
Definizione e proprietà del triangolo rettangolo
Il triangolo rettangolo è una figura geometrica piana composta da tre lati e tre angoli, di cui uno è sempre un angolo retto (cioè di 90 gradi). Le proprietà che caratterizzano questa figura sono fondamentali per comprendere non solo il concetto di area, ma anche per applicare questa conoscenza in contesti pratici.
Caratteristiche principali
- Ipotenusa: il lato opposto all’angolo retto, ed è il lato più lungo del triangolo.
- Cateti: i due lati che formano l’angolo retto.
- Teorema di Pitagora: afferma che in ogni triangolo rettangolo, il quadrato dell’ipotenusa è uguale alla somma dei quadrati dei cateti.
Le suddette caratteristiche non solo definiscono la forma del triangolo rettangolo ma sono anche essenziali nel calcolo dell’area, come vedremo nei paragrafi successivi.
Formule per il calcolo dell’area
Per determinare l’area di un triangolo rettangolo, si può utilizzare una formula semplice e diretta, che è il risultato della metà del prodotto dei cateti. Questa formula deriva direttamente dalla definizione generale dell’area di un triangolo, ma assume una forma particolare grazie alla presenza dell’angolo retto.
Formula dell’area
L’area AAA di un triangolo rettangolo può essere calcolata utilizzando la seguente formula:
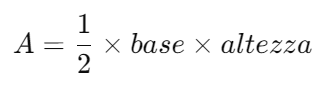
Dove la base e l’altezza nel caso del triangolo rettangolo corrispondono ai due cateti.
Applicazioni pratiche del calcolo dell’area
Il calcolo dell’area di un triangolo rettangolo trova numerose applicazioni nel mondo reale. Queste includono, ma non sono limitate a, la progettazione architettonica, la trigonometria nella navigazione, e l’analisi di strutture e forze in ingegneria.
Esempi di applicazioni
- Architettura: l’utilizzo dei triangoli rettangoli per calcolare inclinazioni e spazi in progetti di costruzioni.
- Navigazione: l’uso della trigonometria, che si basa sulle proprietà dei triangoli rettangoli, per determinare la posizione e la rotta di navi e aerei.
Esercizio guidato calcolo area triangolo rettangolo con disegno
In questo esercizio, impareremo come calcolare l’area di un triangolo rettangolo utilizzando i cateti come base e altezza. Seguiremo passo dopo passo il processo, completato con un disegno che illustra il triangolo rettangolo con i cateti di lunghezza 3 cm e 4 cm.
Passaggi dell’esercizio:
Considera il disegno fornito per avere una rappresentazione visiva del problema e della soluzione.
Riconoscere le dimensioni e la forma:
Disegna un triangolo rettangolo con un angolo retto.
Etichetta i cateti, i due lati che formano l’angolo retto, con le misure:
Un cateto (base) di 3 cm.
L’altro cateto (altezza) di 4 cm.
Impostare la formula dell’area:
L’area AAA di un triangolo è data dalla formula:
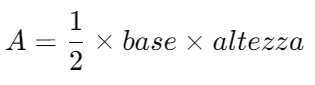
Sostituisce le dimensioni dei cateti nella formula:
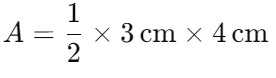
Calcolare l’area:
Esegui il calcolo:
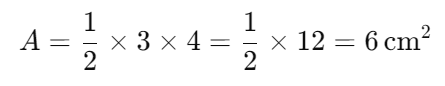
Quindi, l’area del triangolo rettangolo è di 6 cm².
Esercizi sul Calcolo dell’Area del Triangolo Rettangolo
Ecco una serie di esercizi per praticare il calcolo dell’area dei triangoli rettangoli, completi di soluzioni dettagliate. Questi esercizi sono pensati per consolidare la comprensione e l’applicazione della formula dell’area.
Esercizio 1
Un triangolo rettangolo ha un cateto di 5 cm e l’altro di 12 cm. Calcola l’area del triangolo.
Esercizio 2
Un triangolo rettangolo ha un’ipotenusa di 13 cm e uno dei cateti è 12 cm. Trova l’area del triangolo.
Esercizio 3
Calcola l’area di un triangolo rettangolo i cui cateti misurano rispettivamente 8 cm e 6 cm.
Esercizio 4
Se l’area di un triangolo rettangolo è 50 cm² e un cateto è lungo 10 cm, trova la lunghezza dell’altro cateto.
Esercizio 5
Un triangolo rettangolo ha cateti che misurano 9 cm e 40 cm. Determina l’area del triangolo.
Soluzioni
- Soluzione 1: 30cm2
- Soluzione 2: 30cm2
- Soluzione 3: 24cm2
- Soluzione 4: 10cm
- Soluzione 5: 180cm2
